Young’ın çift-yarık deneyi ışığın dalgaboyunun ilk ölçümlerini vermekteydi. Ancak bu ölçümlerde interferans örneklerinin maksimum ve minumum yerleri oldukça zor tesbit edilmekteydi. Bundan dolayı da Young’ın deneyi oldukça düşük hassasiyetli sonuç vermektedir. Şimdi, dalgaboyu ölçümünü son derece hassas bir şekilde veren bir yol tanımlayacağız. Bu yöntem çift yarık deneyinin genişletilmesine dayanmaktadır. Birbirine son derece yakın çok sayıda paralel yarık ihtiva eden ve şebeke (grating) olarak isimlendirilen bir alet kullanılır. Şebekenin tam teorisi gayet karmaşık olduğundan, burada sadece bazı en önemli kısımları incelenecektir.
Bir şebeke (genellikle difraksiyon şebekesi olarak isimlendirilir) keskin bir elmas uç kullanılarak düz bir cam plak üzerine çok sayıda ince paralel oyukların kazınmasıyla oluşturulur. Oyuklar geçirgen (opak) değildir ve plak üzerine düşen ışık sedece oyuk olmayan kısımlardan serbest bir şekilde geçer. Böylece, bu kısımlar bir yarık olarak rol oynar. Böyle bir alet geçirgen (transmission) şebeke olarak isimlendirilir. (Yansıtıcı –reflection- şebekeler düz sırlanmış bir metal yüzey üzerine oyuk açılmasıyla yapılır ve yapılan deneyde yansıyan ışık kullanılır. Her iki şebeke türü de aynı teoriyi kullanır.) Görünür ışık kullanıldığında iyi bir şebekede milimetre başına 500 ila 1500 oyuk veya çizgi bulunur.
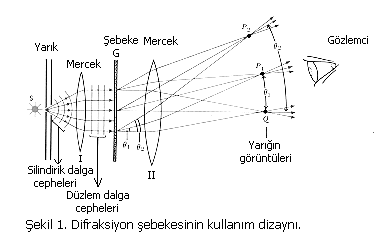
Şimdi bir şebekenin nasıl kullanıldığını görelim. Şekil 1 ölçekli olmamakla beraber difraksiyon şebekesi için tipik bir dizayndır.

Deneyde bir S kaynağı incelenecektir. Şimdilik kaynağın l dalgaboylu monokromatik bir kaynak olduğunu varsayalım. S ‘den gelen ışığın bir kısmı dar düşey bir yarıktan (sayfa düzlemine dik) geçer. Bu yarık Young deneyindeki gibi aynı fonksiyonu görür. Yani, silindirik dalga cepheleri yayınlayan koherent bir çizgi kaynağı gibi rol oynar. Işık daha sonra I merceği üzerine düşer. Bu mercek ışınları düzlem paralel dalga cephesine çevirir. Bu durumda mercekten geçen koherent ışık koherentlik özelliğini kaybetmez. Böylece G şebekesi üzerine düşen herbir düzlem dalga cephesi koherent ışıktan ibaret olur. G bir çok düşey eşit aralıklı yarık ihtiva eden geçirgen bir şebekedir. Huyghens prensibine göre şebekedeki yarıkların herbiri koherent ışığa sahip bir çizgi kaynak gibi rol oynar ve G ‘nin sağ tarafına silindirik dalgacıklar gönderir. Bu ışınlar Q, P1, P2 gibi yerlerde görüntüler oluşturmak üzere II merceği tarafından toplanır. Bu görüntülerin her biri gözlemciye ekranda aydınlatılmış yarık gibi görünür; herbiri düşey parlak çizgidir. Bu çizgi görüntüler mertebe olarak isimlendirilir. Sistemin optik ekseni üzerindeki Q noktasındaki mertebe sıfırıncı mertebedir. Mertebeler P1 ‘de birinci mertebe, P2 ‘de ikinci mertebe şeklinde devam eder. İkinci mercek tarafından oluşturulan herbir mertebenin SQ ekseniyle özel bir açıda paralel ışınlar seti oluşturduğuna dikkat edilmelidir. Böylece, P1 ‘deki mertebe şebekeden çıkıp eksenle q1 açısı yapan ışınlar tarafından oluşturulurken, Q ‘da oluşan mertebe şebekeden eksene paralel gelen ışınlar tarafından oluşturulur. Şimdi, şebekenin, mertebeleri nasıl ve nerede oluşturduğuna bakalım.
Şekil 2, G şebekesinin küçük bir kısmının büyütülmüş bir kesitini ve şebeke üzerindeki bir çok yarıktan sadece A, B, ... , E gibi bir kaç yarığı gösterir.
Herbir yarık silindirik Huygnes dalgacıkları üretir. Gözlenen görüntüyü oluşturan da (toplandıktan ve II merceği tarafından odaklandıktan sonra) bu dalgacıklarda oluşan ışığın girişimidir. W0 düzlem dalga cephesi, birbirlerine göre sıfır faz kayması gösteren bu dalgacıklara teğet olarak çizilir. Bundan dolayı W0 sol tarafta G ‘den gelen sapmamış ışınları ihtiva eder. Merkezi hat boyunca R0 olarak gösterilen bu ışınlar Şekil 1’de Q noktasındaki mertebeyi oluşturlar.
Şekil 2 ‘deki W1 dalga cephesi şu şekilde çizilir. W1, A yarığında başlar ve B yarığının sağında çizilen ilk dalgacığa teğettir. Geometriden W1 keza C ‘den çizilen ikinci dalgacığa, D ‘den çizilen üçüncü dalgacığa ve bu şekilde devam ederek diğer dalgacıklara teğet olur. W1, R1 ile gösterilen ışınlar setine karşılık gelir. Bu koherent yani aynı fazdaki ışınların tamamı eksenle q1 açısı yapar. Bu ışınlar Şekil 1 ‘deki P1 noktasında birinci mertebe olarak isimlendirilen parlak çizgiyi oluşturmak üzere II merceği tarafından toplanırlar.
Şekil 2 ‘deki W2 dalga cephesi aşağıda anlatıldığı şekilde oluşur. W2, A yarığında başlar ve B yarığının sağında çizilen ikinci dalgacığa teğettir. Böylece C ‘nin sağındaki dördüncü dalgacığa, D ‘nin sağındaki altıncı dalgacığa ve bu şekilde devam ederek diğer dalgacıklara da teğet olur. R2 ile gösterilen bu ışınların hepsi eksenle q2 açısı yapar ve W2 dalga cephesine karşılık gelir. II merceği tarafından toplanan ve dolayısıyla kuvvetlendirilen bu aynı fazdaki ışınlar Şekil 1 ‘deki P2 noktasında ikinci mertebeyi oluştururlar.
Böylece, gözlemci, II. mercekten geçen ışınların toplanarak son derece şiddetli mertebeler seti oluşturduğunu görür. Şayet gözlemci Şekil 1’deki SQ ‘nun altına eksenin diğer tarafına bakarsa özdeş bir yapı görecektir. Q ‘daki sıfırıncı mertebe hariç bütün mertebeler eksenin her iki tarafında simetrik çiftler oluşturur.
Şimdi mertebelerin yerlerini belirlemek için bir bağıntı çıkaralım. Eksenden itibaren ölçülen qn açısı ve oluşan mertebe sayısı (n) için bir ifade elde etmek istiyoruz. Şekil 3, sadece Şekil 2 ‘deki A, B ve C yarıklarının biraz daha büyütülmüş bir kesitini göstersin.
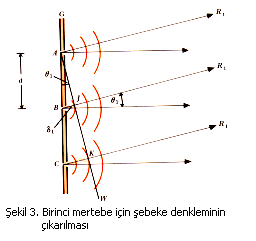
AW1 birinci mertebeyi veren W1 dalga cephesinin bir kısmıdır. R1 ışınları, AJB, AKC gibi dik açılar oluşturan W1 ‘in normalidir. BAJ açısı q1 ‘dir. Bitişik yarıklar arasındaki d açıklığı şebeke boşluğu (grating spacing) olarak isimlendirilir.
d = AB = BC = ...
Kritik uzaklık,
d1 = BJ
dir. Şayet d1 = l, kaynaktan gelen ışığın dalgaboyu ise bu durumda CK = 2l ve bu şekilde devam eder. Sonuçta R1 ‘e ait bütün ışınlar aynı fazda olurlar.
d1 = d sin q1
olduğundan, q1 için gerekli şart,
sin q1 = l / d
olur. Benzer yol kullanılarak Şekil 2 ‘deki W2 dalga cephesi için,
d2 = 2l = d sin q2,
veya
sin q2 = 2l / d
bulunur. Genelleştirirsek, n mertebesi qn açısında oluşur. Böylece şebeke denklemi olarak isimlendirilen,
sin qn = n l / d (1)
bağıntısını elde ederiz.
Problem-1: Şekil 1 ‘deki S kaynağının sodyum lambası (l = 5.893´10-7 m) olduğunu varsayalım. G şebekesinin uzunluğu boyunca her santimetresinde 5000 çizgi (yarık) bulunduğuna göre gözlenebilecek bütün mertebelerin açısal konumlarını bulunuz.
Çözüm-1: Önce d şebeke boşluğu hesaplanır. Şebekede 5000 yarık/cm veya 5´105 yarık/m vardı. d, bitişik yarıklar arasındaki uzaklık olduğundan her bir yarık arasındaki uzaklık d = 1 / 5´105 = 0.000002 veya d = 2´10-6 m ‘dir. Şimdi mertebeler arasındaki açıyı tayin edelim. Şüphesiz sıfırıncı mertebe daima merkezde olacağından her hangi bir l ve her hangi bir d için q0 = 0° dir. Şebeke denkleminden,
Birinci mertebe: sin qn = n l / d
sin q1 = (1) ´ 5.893´10-7 m / 2´10-6 m = 0.295, q1 = 17°.2 ;
İkinci mertebe:
sin q2 = (2) (0.295) = 0.590, q2 = 36°.2 ;
Üçüncü mertebe:
sin q3 = (3) (0.295) = 0.885, q3 = 62°.2 ;
Dördüncü mertebe:
sin q4 = (4) (0.295) > 1 dördüncü mertebe oluşmaz.
Böylece, bu problemdeki verilere göre sadece üç (çift) mertebe gözlenir.
NOT: Mertebeler arasındaki boşluğun artan mertebe sayısıyla nasıl arttığına dikkat edelim. q1 - q0 = 17° , q2 - q1 = 19° , ve q3 - q2 = 26° .
Problem-2: Önceki problemdeki şebekeyi kullanarak l1 = 4´ 10-7 m (mor) ve
l2 = 5 ´ 10-7 m (mavi) gibi iki dalgaboyunda ışınım yapan bir kaynağı inceleyelim. Ne gözleriz?
Çözüm-2: Her bir dalgaboyu, şebeke denklemine göre kendi mertebeler setini oluşturur.
Mor için, l1 / d = (4´ 10-7)/(2´ 10-6) = 0.200.
Mavi için, l2 / d = (5´ 10-7)/(2´ 10-6) = 0.250.
Sıfırıncı mertebede bütün l ‘lar için q0 = 0 olduğundan spektrel renkler arasında bir boşluk yoktur ve bundan dolayı sıfırıncı mertebede oluşan renk kaynakla aynı renktedir. Şebeke denkleminden; sin qn = n l / d
Birinci mertebe:
Mor : sin q1 = (1) ´ (0.200) = 0.200, q1 = 11°.5 ;
Mavi : sin q1 = (1) ´ (0.250) = 0.250, q1 = 14°.5 ;
İkinci mertebe:
Mor : sin q2 = (2) ´ (0.200) = 0.400, q2 = 23°.5 ;
Mavi : sin q2 = (2) ´ (0.250) = 0.500, q2 = 30°.0 ;
Üçüncü mertebe:
Mor : sin q3 = (3) ´ (0.200) = 0.600, q3 = 36°.9 ;
Mavi : sin q3 = (3) ´ (0.250) = 0.750, q3 = 48°.6 .
Dispersiyon: Burada sıfırıncı mertebe hariç, mor ışın mavi ışından daha az sapmak üzere herbir mertebe bir spektrel çizgi çiftinden oluşmuştur. Açısal ayrıklık veya dispersiyon herbir spektrel çizgi çifti için mertebeyle artar. Şekil 4, Şekil 1 ‘deki gözlemci tarafından görünen spektrel çizgilerin konumlarını gösterir. Şayet II merceğinin görüntüsü düşey bir ekran üzerinde görülecek şekilde projekte edilirse spektrel çizgiler Şekil 5 ‘deki gibi görülür.
Problem-3: Şekil 1 ‘deki S kaynağının, kırmızıdan (lR = 7´ 10-7 m) mora
(lv = 4´ 10-7 m) görünür tüm dalgaboylarından ibaret beyaz ışık ürettiğini varsayalım. Gözlenen görüntüyü tanımlayınız.
Problem-4: 1´ 10-10 m X-ışın dalgaboyunun birinci mertebesinin eksenden 30° ‘de görülmesi için şebeke boşluğunun (iki çizgi arasındaki mesafenin) ne olması gerekir?
Şu ana kadar çok yarıklı bir şebekenin Young deneyinde görülenden bir kaç daha fazla mertebe ürettiğini gördük. Aynı zamanda bu şebeke mertebeleri hem daha geniş hem de birbirlerinden oldukça ayrıktı. Henüz şebeke tarafından üretilen spektrel çizgilerin ne kadar keskin oluştuğunu görmedik. Bunun nasıl ortaya çıktığını görmek için Şekil 6 ‘da verilen tarzda bir çeşit genlik-faz diyagramı oluşturmak faydalıdır. Önce herbir mertebesi bir tek çizgi olan monokromatik bir kaynak gözönüne alalım. Şekil 1 ‘deki her hangi bir şebeke yarığından II merceğine doğru eksenle belirli bir q açısı yapan ışığın genliğini kısa bir A vektörüyle temsil ettiğimizi varsayalım.
Bütün yarıklardan gelen katkı q0 = 0° için aynı fazdadır, şöyle ki, Şekil 6a ‘da görüldüğü gibi genlik vektörleri paraleldir. q0 = 0° ‘da ortaya çıkan genlik böylece NA olur. Burada N şebekedeki yarıkların toplam sayısıdır. q0 = 0° ‘da çok şiddetli sıfır mertebesi veren büyük bir kuvvetlenme olur. Bir kez daha Şekil 2 ve Şekil 3 ‘e dönelim ve q ‘nın bir yay dakika gibi küçük bir açıdaki bir dalga cephesini gözönüne alalım. Bu küçük açıya Δq diyelim. Bu küçük açıda B yarığından gelen A genlik katkısı A yarığından gelene göre küçük bir faz farkı vardır. Bu faz farklarını aşağıdaki gibi hesaplayabiliriz. Δq ‘ya karşılık gelen faz farkı Şekil 3 ‘deki AJB üçgeninden,
Δd = d sin Δq
dır. Bu yol farkına karşılık gelen dalgaboyunun kesri,
Δd / l = d sin Δq / l,
Δq ‘ya karşılık gelen A ve B yarıklarından gelen ışınlar arasındaki Δf faz farkı
Δf = Δd (2p) / l = 2p d sin Δq / l,
Δq küçük açı olduğundan, bu son ifadeyi,
Δf » 2p d Δq / l,
şeklinde yazabiliriz.
Örneğin Δq = 1¢ » 3´10-4 rad, d = 2´10-6 ve l = 4´10-7 m ise ardışık yarıklardan gelen katkılar arasındaki faz farkı,
Δf » 2p d Δq / l = 2p ´ 2´10-6 ´ 3´10-4 / 4´10-7 » 10-2 rad » 0°.6 .
Bunun anlamı, eksenden yaklaşık 1 yay dakika hareket ettiğimizde, B yarığından gelen A genliğinin A yarığından gelenle 0°.6 faz dışında olduğudur. Benzer şekilde C yarığından gelen A genliği B yarığından gelenle 0°.6 faz farklıdır ve yarıklar arasındaki durum böylece devam eder. Şimdi artık genlik-faz diyagramı Şekil 6b ‘ye benzer. Bu diyagram N tane eşit genlikli vektörlerin ilave edilmesiyle oluşur. N çok büyük olduğundan dolayı Δf çok küçük olsa bile ortaya çıkan sonuç, ΣA ‘nın NA ‘dan çok daha küçük olduğu şeklindedir. Örneğin, santimetresinde 10 000 çizgi bulunan 5 cm boyundaki bir şebekede N = 50 000 ‘dir. Şayet NΔf = 2p ise bu durumda vektör diyagram kapalıdır. Şekil N-kenarlı bir poligona benzer. ΣA = 0 dır.
Bütün bunların sonucu şunu göstermektedir ki, şebeke denklemi tarafından hesaplanan mertebelerden birinin çok küçük bir açısal yer değiştirmesi ışığın genliğinde, dolayısıyla şiddetinde çok keskin bir düşmeye neredeyse mertebenin bulunduğu yerin tamamen karanlığa dönüşmesine neden olur. Bu durum çok keskin mertebeler oluşturur. İlave olarak, bu durum çok parlak mertebeler de oluşturur. Çok fazla sayıdaki dalganın birbirlerine göre az da olsa bir faz farkı olması sonucu ortaya çıkan girişim mertebeler arasında karanlık bölgelerin oluşmasına neden olur. Dalgalar tarafından taşınan enerji hesaba katılmalıdır. Mertebeler, oldukça siyah bir zemin üzerinde göze batacak kadar parlak ve keskin görünür (Şekil 5).
Bütün mertebeler eşit parlaklıkta değillerdir. Yüksek mertebelere baktığımız zaman, Young deneyinde olduğu gibi şiddette bir azalma olur. Huyghens prensibinin tam formülü bu etkiyi açıklar.
Spektrel çizgilerin ayırmagücü
Bir şebekenin spektrel çizgileri ayırma veya ayrıştırma kabiliyetinin bilinmesi önemlidir. İyi bir ayırmagücünün anlamı, birbirlerine çok yakın ışık dalgalarını aralarındaki mesafeyi ölçebilecek kadar (verilen bir mertebede) yeterli ayrıştırılabilmesidir. Birinci mertebeyi göönüne alalım. Verilen bir l için birinci-mertebe maksimum şebeke denklemine göre (l = d sin q) bir q açısında oluşur. Bir sonraki aşamada tamamen yok edici girişimin oluştuğu q ‘ya en yakın açıyı bulalım. Toplam bozulma, Şekil 6 ‘daki genlik faz diyagramı kapalı bir polinom (Δf = 2p/N) olduğu zaman oluşur. l durumunda bu şart,
l + l/N = d sin qmin (2)
olur.
Şimdi artık şebeke üzerine gelen ışığın l ‘ya yakın l¢ dalgaboylu ikinci bir bileşen ihtiva ettiğini kabul ederiz. Bu iki dalgaboyunun ayırt edilip edilemeyeceğini bilmek isteriz. Birbirlerinin yeri genişliğinden daha fazla bir üstüste çakışma olmazsa spektrel çizgilerin ayırd edilebileceğini bulunmuştur. Bu ayırma sınırı Şekil 7 ‘de görmek mümkündür. Şekle dikkatli bakıldığında l¢ dalgaboylu çizginin maksimumunun l dalgaboylu çizginin mimumumuna (qmin ) karşılık geldiği görülür. l¢ dalgaboyu çizgisi için şebeke denklemi, birinci-mertebe maksimumun yerini,
l¢ = d sin qmin (3)
bağıntısıyla verir. (2) ve (3) nolu bağıntılar birleştirilerek,
l + l/N = l¢
veya
l¢ - l / l = 1/N = Dl/l, (4)
bulunur. Burada Dl, l¢ - l dalgaboyu farkıdır.
(4) nolu bağıntı bize, N ‘nin değeri ne kadar büyükse yani şebekedeki toplam çizgi sayısı ne kadar fazlaysa, Dl/l dalgaboyu farkının o kadar küçük olacağını söyler. Sonuç olarak N ‘nin fazla olması şebekenin ayırmagücünün artacağı anlamına gelir.
Problem 5: Bir şebekenin santimetresinde 1000 yarık vardır. Sodyum spektrumundaki birbirine yakın sarı D çizgilerinin ancak birbirlerinden ayrılabilmesi için şebeke ne kadar büyük olmalıdır? Çizgilerin dalgaboyları: 5.890 ´ 10-7 m ve 5.896 ´ 10-7 m ‘dir.
Çözüm 5: (4) nolu bağıntıdan 1/N = Dl/l ; buradan ;
5.890 ´ 10-7 m - 5.896 ´ 10-7 = 0.006 ´ 10-7 m
N = l / Dl = 5.890 ´ 10-7 / 6 ´ 10-10 » 1 000 çizgi
Demek ki 1 cm boyunda bir şebeke gereklidir.
Problem 6: Hidrojenin Balmer serisinin Ha çizgisinin dalgaboyu 6.562793 ´ 10-7 m hassasiyetle ölçülebilmektedir. Bu, yaklaşık 10-13 m ‘lik bir belirsizlikle ölçüldüğü anlamına gelmektedir. Santimetresinde 10 000 yarık bulunan bir şebeke gözönüne alındığında, 10-13 m dalgaboyu farkı olan iki spekterl çizgiyi ayırd edebilmek için bu şebekenin boyu ne olmalıdır.
Çözüm 6: N = l / Dl = 6 ´ 10-7 / 10-13 = 6 ´ 106 çizgi
Gerekli şebekenin boyu ; 6 ´ 106 yarık / 104 yarık/cm = 600 cm = 6 m.