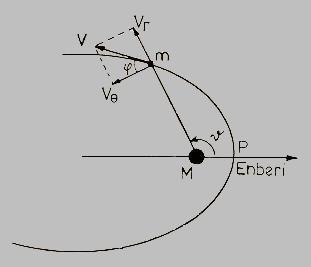
Küçük bir cismin yörüngesi üzerinde verilen herhangi bir noktadaki hızı ve bu hızın doğrultusu nedir? Uydu ve çekim etkisinde bulunan cisim (Yer, gezegen, vs) ikili bir sistem oluştururlar. Sorun iki cisim problemidir.

Yukarıdaki şekilde M kütleli bir cisim etrafında dolanan m kütleli bir uydu gösterilmiştir. Buna göre V yörünge hızı, V teğetsel hız, V_r dikine (radyal) hız, ise yörünge hızının durum açısıdır. Şimdi elimizdeki parametreleri ve denklemleri sıralayalım.

Tanımlar:

	Yarıçap vektörünün sayısal değeri: r
	Gerçek ayrıklık : n
	Yörünge yarı-büyük eksen uzunluğu : a
	Yörünge dış merkezliği : e
	Eylemsizlik sabiti : µ

            Bu tanımların matematiksel ifadelerini yazalım:

	Yörüngenin Genel Denklemi:
	Yörüngenin parametresi:
	Eylemsizlik sabiti:
	Alan sabiti:

Bu verilenler kullanılarak istenen terimler: , teğetsel hız bileşeni; V_r , dikine hız bileşeni ve V nin durum açısı dir. Amacımız yörüngeye ait genel hız bağıntısını bulmaktır.

elde edilir. Bu (5) nolu denkleme genel hız denklemi denir. Buraya kadar yapılanları özetlersek, genel hız denkleminden birçok yörünge üyesini tespit etmek mümkündür.

SONUÇ:    µ, r, a ve e değerleri biliyorsa V hızı bulunabilir.

		denkleminden p değeri,
		denkleminden h değeri,
		denkleminden Vr teğetsel hız değeri,
		denkleminden dikine hız değeri,
		denkleminden de V değeri hesaplanabilir.

(5) denklemini şimdi çeşitli yörünge türlerine uygulayalım.



ÇEŞİTLİ YÖRÜNGELERDE HIZ BAĞINTILARI


1) Dairesel Yörüngeler

Dairede a = r = sabit olduğundan, V_r= 0, dolayısıyla = 0 olduğundan,

Eliptik bir yörüngede (elips) dolanan bir uydunun elipsin odaklarına olan uzaklığı devamlı değişmektedir. Odaklardan birinde bir gezegen bulunmaktadır. Dolayısıyla uydunun hızıda yörünge üzerinde sabit olmayıp devamlı değişmektedir. Elips şeklindeki bir yörüngede perihel, apel, küçük eksen uçları ve herhangi bir yerdeki hızlar farklı olmaktadır.

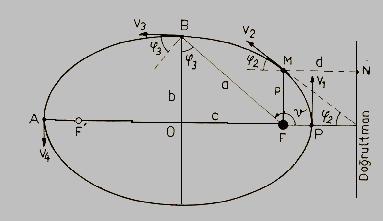
Yukarıdaki eliptik yörüngelerdeki P, enberi (perihel), A enöte (afel), M parametri ucu, B ise küçük eksen ucunu göstersin. Şimdi bu noktalarda genel hız denkleminin ifadesini görelim.

a) Enberi noktası:

b) Parametre ucundaki, (M noktasındaki) durum:

c) Yarı-küçük eksen ucunda, B noktasındaki durum:

d) En Öte noktasında, yani A noktasında,

4) Parabolik yörüngelerde:

HIZDAN YÖRÜNGE HESABI

Yer yörüngesine oturtulmak istenen bir uydu, önce geçici bir yörüngeye oturtulur. Bu geçici yörünge daire veya daireye yakın bir elipstir. Uydunun yerden uzaklığı oldukça azdır. Uydu bu geçici yörüngede belli bir süre tutulduktan sonra istenilen kendi yörüngesine oturtulur. Yörünge değişimi eski yörüngesindeki hız ve uydunun sahip olduğu potansiyel enerji göz önüne alınarak yapılır. Geçici yörüngesinin uygun bir yerinde (genellikle enberi noktasında) yörünge motorları kısa süre çalıştırılarak yeni bir hız kazandırılır. Uydu yeni bir hız ve potansiyel enerjisindeki değişimden dolayı kendine yeni bir yörünge çizer. Bu yörünge uydunun gerçekte oturtulmak istendiği yörüngedir.

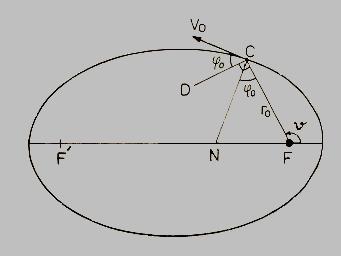
	Eylemsizlik sabiti:	µ = G (M+m)
		M: Yer veya gezegen kütlesi
		m: Uydunun kütlesi
	Fırlatma uzaklığı:	ro
	Fırlatma hızı:	Vo
	Fırlatma durum açısı:	o

	Alan sabiti:
	Parametre:
	Yarı büyük eksen:
	Dışmerkezlik:
	Dolanma peryodu:

Verilen  µ, r_o ve V_o, _o değerlerine göre yeni yörüngenin şeklinin belirlenmesi.


1. Adım:

V_c, V_p ve a bilindiğine göre yörüngenin şekli hakkında bir kanıya varabiliriz:

a) _o = V_c olduğunda = 0 olursa, e = 0 olur. Yörünge dairedir.

b) _o = V_c olduğunda 0 < < 90 ise e < 1 olur. Yörünge elipstir.

c) _o = V_c iken = 90 ise (fırlatma yarçap doğrultusunda), e = ±1 olur. Yörünge bozulmuş bir paraboldur.

4. Adım:

Eğer fırlatma yarıçapa dik yani   = 0 ise,

bağıntısı elde edilir. Bu durumda yeni yörünge elips, daire ve parabol yörüngeler olabilir. Aşağıdaki dört şekil farklı fırlatma açılarına göre oluşabilecek yeni yörüngeleri göstermektedir.

	Önceki Konu	Ana Sayfa	Sonraki Konu